Chapter 4 Summary

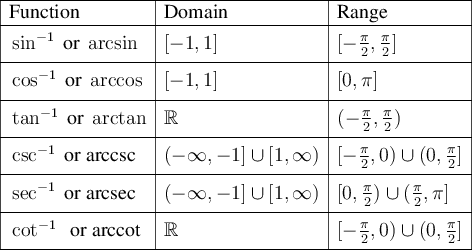
Chapter 4 is composed of 11 sections. All of them are very challenging concepts to be absorbed. We learned the trig identities of sine, cosine, and tangent; the trig graph; verifying trig identities; inverse trig functions; harmonic motion. Among these various lesson, I think I am pretty confident on 4.8: Inverse Trigonometric Functions. From researching the definition, I found out that In mathmatic, the inverse trigonometric functions (occasionally called cyclometric functions) are the inverse functions of the trigonometric functions (with suitably restricted domains). For example, a question is asked to find the inverse function of sine that's equal to 1/2. The answer would be pi/6. We could answer this in a complete sentence "the angle whose sine is 1/2 is pi/6". The algebraic abbreviation for that sentence is arcsine=pi/6.

Mr.Unit Circle

The "Unit Circle" is a circle with a radius of 1. Frequently, especially in trignometry, the unit circle is the circle of radius one centered at the origin (0, 0). Being simple, it is a way to learn and talk about lengths and angles. The center is put on a graph where the x axis and y axis cross, so we get this neat arrangement here. Because the radius is 1, we can directly measure sine, cosine, and tangent.
For example:
What happens when the angle, θ, is 0°?

• cos 0° = 1, sin 0° = 0 and tan 0° = 0

What happens when θ is 90°?

• cos 90° = 0, sin 90° = 1 and tan 90° is undefined

Law of sines Law of cosines

This week we learned the law of sines and the law of cosines. In trigonometric, the law of sines is an equation relating the lengths of the sides of any shaped triangle to the sines to its angles. According to the law, a/sine A=b/sine B=c/sine C, where a,b, and c are the lengths of the sides of a triangle, and A, B, C are the opposite angles. Law of cosines is an equation relates the lengths of the sides of a triangle to the cosine of one of its angles. The law of cosines generalize the Pythagorean theorem, which holds only for right angles. 

Trigonometric equation

A trigonometric equation is any equation that contains a trigonometric function. In order to solve a trig equation, we have to use both the reference angle we have memorized and a lot of algebra we have learned. For example, solve sin(x)+2=3 for 0 degree < x< 360 degree. I'll first isolate the variable containing term. Sin(x)+2=3 sin(x)=1. Now I'll use the reference angle I have memorized x=90.

Verifying identities

We have different identities to deal with the trig formulas, and those identities makes it easier to solve. For example, sin^2x+cos^2x=1, and 1+tan^2x=sec^2x. In order to solve the problem completely, we should use some rules, first simplify more complicated side. Second, we should find their common denominators if it is possible. We should always change all trig function in terms of sine and cosine. And finally, we can try to plug them into the identities we learned this week. 

Tangent functions and graph

We learned how to solve and graph tangent equation. The tangent will be undefined wherever it's denominator is zero. The tangent wil be zero wherever it's numerator is zero. Therefore, the tangent will have vertical asymptotes wherever the cosine is zero. One basic knowledge about tangent is that it equals to sin/cosine. 

Chapter 3 review

We basically learned how to deal with polynomial function, long division, synthetic division, rational zero test, finding approximating zeros, and rational functions. For polynomial function, we learned that the a i are real numbers and are called coefficients, also the term an is assumed to be nonzero and is called the leading term. Then we learned how to use long division and synthetic division and we can use both way to divide functions. For approximating zeros, we divide the interval in half to find its midpoint and complete f(m).

Sine and cosine functions

We learned how to deal with sine and cosine fuction this week. The sine and cosine are the two most prominent trigonometric functions. All of other trig functions can be expressed in terms of them. The sine theta is the vertica coordinate of the arc endpoint, and the cosine theta is the horizontal coordinate. 

10/3 What I learned this week: rational function

This week we learned "real zeros of polynomial functions", "approximating real zeros", and "rational functions". Among those new materials, the rational function is the most memorable and abstruse to me. The rational function is a function that one is divided by the other to form a ratio of two polynomials. In order to graph a rational function, it requires the vertical and horizontal asymptotes. For vertical asymptotes, just simply set the denominator of the function equal to zero and solve. For the horizontal asymptotes, it is more complicated. You have to find n^th and m^th degree of the polynomial and according to different conditions, the answer varies. 

What I learned last week

Last week, I learned how to find an absolute value and the distance between two numbers. Continuing on this topic, we later learned that how to find the midpoint and absolute value inequalities. For 1.3, we know how to deal with rectangular coordinate system. We also learn the distance formula to get the distance between two lines.

Zeros of a Function

A value of x which makes a function: f(x) equals to 0 is called zeros of a function. In this circumstances, a zero may be real number or complex number. The first step to find the zeros of a function is to set up the given equation. And find the answer that is to give the equation an "a" ,"b", and "c" number and write down all the factor pairs of the "c" value. The final step is to solve each factor by moving the constant number over.

All about me

My name is Angle Zhang and a current sophomore at MHS. I was born in Arcadia and raised in Shanghai, China. I have a brother who's two years younger than me and goes to Arcadia High school. I love music and movies, especially horror movies. I went to Clairbourn for middle school and graduated in 2013.  

9/12 A piece wise function

A piece wise function can be interpreted as putting a graph in to different pieces. It is more complicated than a normal linear function. Y and x are dependent to each other that for example y is defined differently for different values of x. People often use x as a reference to look up what interval it's in. Therefore they can find out the correspond value for y.

9/5 Superhero Transformation

This blog is to show that how I used those superheros of transformation, how I controlled to move objects around the coordinate plane, and guided the Superheros to overcome their missions. There are six different superhero that lived in 6 family categories: linear, quadratic, exponential, absolute value, square root, and cubing. They holds various super power to defeat evils.  

 

 

8/29/14 Week 2 What is a function

A function can be express as f(x)=...... It simply involved one or more variables in just one equation. F(x) in a function can be replaced by y which come out to be y=.......  Also f(x) and set to be equal to y as f(x)=y which in here we make distinction among variable by calling x is the input and y is the output to the function. X can also be called as the independent variable and y as the dependent variable. The value of x has direct affect on the y result. In conclusion, a function can be interpreted as a relationship between variable values, such as x and y.