Chapter 4 Summary

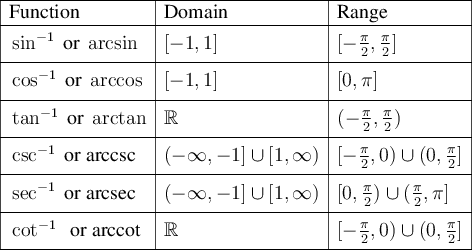
Chapter 4 is composed of 11 sections. All of them are very challenging concepts to be absorbed. We learned the trig identities of sine, cosine, and tangent; the trig graph; verifying trig identities; inverse trig functions; harmonic motion. Among these various lesson, I think I am pretty confident on 4.8: Inverse Trigonometric Functions. From researching the definition, I found out that In mathmatic, the inverse trigonometric functions (occasionally called cyclometric functions) are the inverse functions of the trigonometric functions (with suitably restricted domains). For example, a question is asked to find the inverse function of sine that's equal to 1/2. The answer would be pi/6. We could answer this in a complete sentence "the angle whose sine is 1/2 is pi/6". The algebraic abbreviation for that sentence is arcsine=pi/6.

Mr.Unit Circle

The "Unit Circle" is a circle with a radius of 1. Frequently, especially in trignometry, the unit circle is the circle of radius one centered at the origin (0, 0). Being simple, it is a way to learn and talk about lengths and angles. The center is put on a graph where the x axis and y axis cross, so we get this neat arrangement here. Because the radius is 1, we can directly measure sine, cosine, and tangent.
For example:
What happens when the angle, θ, is 0°?

• cos 0° = 1, sin 0° = 0 and tan 0° = 0

What happens when θ is 90°?

• cos 90° = 0, sin 90° = 1 and tan 90° is undefined

Law of sines Law of cosines

This week we learned the law of sines and the law of cosines. In trigonometric, the law of sines is an equation relating the lengths of the sides of any shaped triangle to the sines to its angles. According to the law, a/sine A=b/sine B=c/sine C, where a,b, and c are the lengths of the sides of a triangle, and A, B, C are the opposite angles. Law of cosines is an equation relates the lengths of the sides of a triangle to the cosine of one of its angles. The law of cosines generalize the Pythagorean theorem, which holds only for right angles.