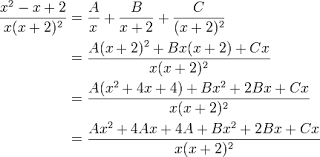2nd Semester Summary

Since it's almost the end of the school year, I want to summary my achievement in math from Honors Math Analysis. So far, I gain some further understanding in math such as trigonometry, repeating decimals and so on. I learned a lot of math solving skills from this class and I think those will be my treasure in future math studies.  Looking back at my previous blogs, I can't believe the amount of math lessons we've covered in this school year! We learned parabolas, rotating conic sections, polar coordinates, graphs of polar equations, system of equations, cramer's rule, graphing systems of inequalities. sequences and series from the first semester. In the second semester, we've covered partial fractions and parametric equations and repeating decimals. I am very thankful to Miss V who's dedicated, cheerful and extremely sweet.

Trig Review Week

Trigonometric is my favorite concept of this entire unit. Trig is basically trigonometric, which is one of the best-known math method is mathland. Trigonometric is a branch of mathematics that studies relationships involving lengths and angles of triangles. Trigonometry is best at find a missing side or angle in a triangle. The 3 most useful special functions Sine, Cosine and Tangent. However, there are total of 6 functions, which is including sine, cosine, tangent, cotangent, cosecant, secant. Also we can always use the unit circle or remember the trig identities to solve the problem.

Repeating Decimals

A decimal number that has digits that repeat forever. The part that repeats is usually shown by placing dots over the first and last digits of the repeating pattern, or sometimes a line over the pattern. The minimum number of digits that repeats in such a number is known as the decimal period. All rational numbers have either finite decimal expansions or repeating decimals . However, irrational numbers, such as pi=3.141592... neither terminate nor become periodic. Numbers such as 0.5 are sometimes regarded as repeating decimals since .

Parametric Equations

From web research, "in mathematics, parametric equations of a curve express the coordinates of the points of the curve as functions of a variable, called a parameter. For example, are parametric equations for the unit circle, where t is the parameter. Together, these equations are called a parametric representation of the curve." Parametric equations are a set of equations that express a set of quantities as explicit functions of a number of independent variables, known as "parameters." For example, while the equation of a circle in Cartesian coordinates can be given by , one set of parametric equations for the circle are given by

Partial Fractions

In class, we learned about partial fraction decompositions. Partial-fraction decomposition is the process of starting with the simplified answer and taking it back apart, of "decomposing" the final expression into its initial polynomial fractions. To decompose a fraction, you first factor the denominator. Then you write the fractions with one of the factors for each of the denominators.
Then you set this sum equal to the simplified result. Multiply things out, and group the x-terms and the constant term. 

Tower of Hanoi

The game The Tower of Hanoi is basically a mathematical game or puzzle that starts with the disks in a neat stack in ascending order of size on one rod, the smallest at the top, thus making a conical shape. Our team tried the game for several times but always takes more steps to complete it. At the end of this game we find an equation show the pattern of this game and can we complete the game perfectly. The equation we prove out is Tn=2^n -1.  The two steps are to show true for n=1 and assume the statement is true for n=k, and prove true for k+1. After we followed these steps to show that k+1 is true and it follows from mathematical induction that the statement is true for every positive integer. For the recursion and mathematical induction, I learned that it is a form of direct proof, and it is done in two steps. The first step, known as the base case, is to prove the given statement for the first natural number. The second step, known as the inductive step, is to prove that the given statement for any one natural number implies the given statement for the next natural number.

Sequences and series

 A sequence is an ordered list of numbers; the numbers in this ordered list are called elements or terms. A series is the value you get when you add up all the terms of a sequence; this value is called the sum. For instance, 1, 2, 3, 4 is a sequence, with terms "1", "2", "3", and "4"; the corresponding series is the sum 1 + 2 + 3 + 4, and the value of the series is 10. A sequence may be named or referred to as A or An.