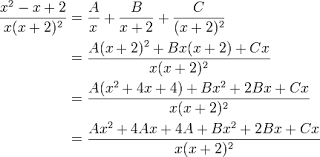2nd Semester Summary

Since it's almost the end of the school year, I want to summary my achievement in math from Honors Math Analysis. So far, I gain some further understanding in math such as trigonometry, repeating decimals and so on. I learned a lot of math solving skills from this class and I think those will be my treasure in future math studies.  Looking back at my previous blogs, I can't believe the amount of math lessons we've covered in this school year! We learned parabolas, rotating conic sections, polar coordinates, graphs of polar equations, system of equations, cramer's rule, graphing systems of inequalities. sequences and series from the first semester. In the second semester, we've covered partial fractions and parametric equations and repeating decimals. I am very thankful to Miss V who's dedicated, cheerful and extremely sweet.

Trig Review Week

Trigonometric is my favorite concept of this entire unit. Trig is basically trigonometric, which is one of the best-known math method is mathland. Trigonometric is a branch of mathematics that studies relationships involving lengths and angles of triangles. Trigonometry is best at find a missing side or angle in a triangle. The 3 most useful special functions Sine, Cosine and Tangent. However, there are total of 6 functions, which is including sine, cosine, tangent, cotangent, cosecant, secant. Also we can always use the unit circle or remember the trig identities to solve the problem.

Repeating Decimals

A decimal number that has digits that repeat forever. The part that repeats is usually shown by placing dots over the first and last digits of the repeating pattern, or sometimes a line over the pattern. The minimum number of digits that repeats in such a number is known as the decimal period. All rational numbers have either finite decimal expansions or repeating decimals . However, irrational numbers, such as pi=3.141592... neither terminate nor become periodic. Numbers such as 0.5 are sometimes regarded as repeating decimals since .

Parametric Equations

From web research, "in mathematics, parametric equations of a curve express the coordinates of the points of the curve as functions of a variable, called a parameter. For example, are parametric equations for the unit circle, where t is the parameter. Together, these equations are called a parametric representation of the curve." Parametric equations are a set of equations that express a set of quantities as explicit functions of a number of independent variables, known as "parameters." For example, while the equation of a circle in Cartesian coordinates can be given by , one set of parametric equations for the circle are given by

Partial Fractions

In class, we learned about partial fraction decompositions. Partial-fraction decomposition is the process of starting with the simplified answer and taking it back apart, of "decomposing" the final expression into its initial polynomial fractions. To decompose a fraction, you first factor the denominator. Then you write the fractions with one of the factors for each of the denominators.
Then you set this sum equal to the simplified result. Multiply things out, and group the x-terms and the constant term. 

Tower of Hanoi

The game The Tower of Hanoi is basically a mathematical game or puzzle that starts with the disks in a neat stack in ascending order of size on one rod, the smallest at the top, thus making a conical shape. Our team tried the game for several times but always takes more steps to complete it. At the end of this game we find an equation show the pattern of this game and can we complete the game perfectly. The equation we prove out is Tn=2^n -1.  The two steps are to show true for n=1 and assume the statement is true for n=k, and prove true for k+1. After we followed these steps to show that k+1 is true and it follows from mathematical induction that the statement is true for every positive integer. For the recursion and mathematical induction, I learned that it is a form of direct proof, and it is done in two steps. The first step, known as the base case, is to prove the given statement for the first natural number. The second step, known as the inductive step, is to prove that the given statement for any one natural number implies the given statement for the next natural number.

Sequences and series

 A sequence is an ordered list of numbers; the numbers in this ordered list are called elements or terms. A series is the value you get when you add up all the terms of a sequence; this value is called the sum. For instance, 1, 2, 3, 4 is a sequence, with terms "1", "2", "3", and "4"; the corresponding series is the sum 1 + 2 + 3 + 4, and the value of the series is 10. A sequence may be named or referred to as A or An.

Graphing system of inequality

Before learning how to graph system of inequality. We first need to learn the symbols for inequalities: The symbol < means less than. The symbol > means greater than. A system of linear inequalities in two variables consists of at least two linear inequalities in the same variables. The solution of a linear inequality is the ordered pair that is a solution to all inequalities in the system and the graph of the linear inequality is the graph of all solutions of the system.

Cramer's Rule

In linear algebra, Cramer's rule is an explicit formula for the solution of a system of linear equations with as many equations as unknowns, valid whenever the system has a unique solution. It expresses the solution in terms of the determinants of the (square) coefficient matrix and of matrices obtained from it by replacing one column by the vector of right hand sides of the equations.  This section is like a review for me since I can still recall form last year's algebra 2. Cramer’s rule may only be used when the system is square and the coefficient matrix is invertible.

Systems of Equations

A system of equations is a collection of two or more equations with a same set of unknowns. In solving a system of equations, we try to find values for each of the unknowns that will satisfy every equation in the system. There are three types of linear equations: inconsistent, consistent with independent equation and dependent equation. When X = a number, y = a number the system is independent and the equations will have different values of m when both are placed in y = mx + b (slope-intercept) form. When an inconsistent equation, such as 0 = 3,the system is inconsistent and equations will have the same value of m, but different values of b, when both are placed in y = mx + b form. When an identity, such as 5 = 5, the system is dependent and equations will be identical when both are placed in slope-intercept form

Polar coordinate

In mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a fixed point and an angle from a fixed direction. To convert polar into rectangular form we need to know that x=r*cosine-data and y=r*sine-data. If data is greater than zero then the graph is counterclockwise, if the data is less than zero than the graph is clockwise. I also acknowledged Cardioids: these have a graph that is vaguely heart shaped and always contain the origin and Limacons with an inner loop: these will have an inner loop and will always contain the origin.Limacons without an inner loop: these do not have an inner loop and do not contain the origin.

Rotating Conic Section

We learn rating conic section on chapter7.4. We studied conic sections with equations of the form: Ax^2+Bxy+Cy^2+Dx+Ey+F=0. Step 1: find angle cot2pi=(A-C)/B where pi is greater than 0 but smaller than 90 degree. Step 2: replace x and y: x=xprime*cosine-data-yprime*sine-data. y=xprime sine-data+yprime cosine data. Step 3:plug these into the original equation and simplify to solve. There are three constant equation help us to recognize different graph shape. Parabola:B^2-4AC=0.

Ellipse: B^2-4ac smaller than 0. Hyperbola: B^2-4AC greater than 0.

Parabolas

We did parabolas on chapter 7 of this semester. Through researching on internet, I now can identify "parabolas" as the curve formed from all the points (x, y) that are equidistant from the directrix and the focus. The line perpendicular to the directrix and passing through the focus (that is, the line that splits the parabola up the middle) is called the "axis of symmetry". I found this chapter to be relatively interesting since I personally like the graphing section of math a lot. A parabola equation is (x-h)^2=4c(y-k) for vertical shift. (Y-k)^2=(x-h) applies for horizontal shifts. 

My second semester goal

My second semester's goal for this class is that I wish I can be more focus at the lecture contents. I'll do detail review before every quiz or test in order to get a descent grade. I hope I can enjoy the math more and explore more math theories in mathland. I was sometime absent-minded last semester and now looking forward to improve that. For Christmas, my family went on a trip to LAke Tahoe. They had beautiful views but the weather was freezing. In general, my break was quiet peaceful and relaxing. 

My polar equation graph